2nd Place Winner | 4-week Project | Image Recognition
Building a Bangla Handwritten Digit Recognizer from Scratch: A Deep Dive into Custom CNN Implementation
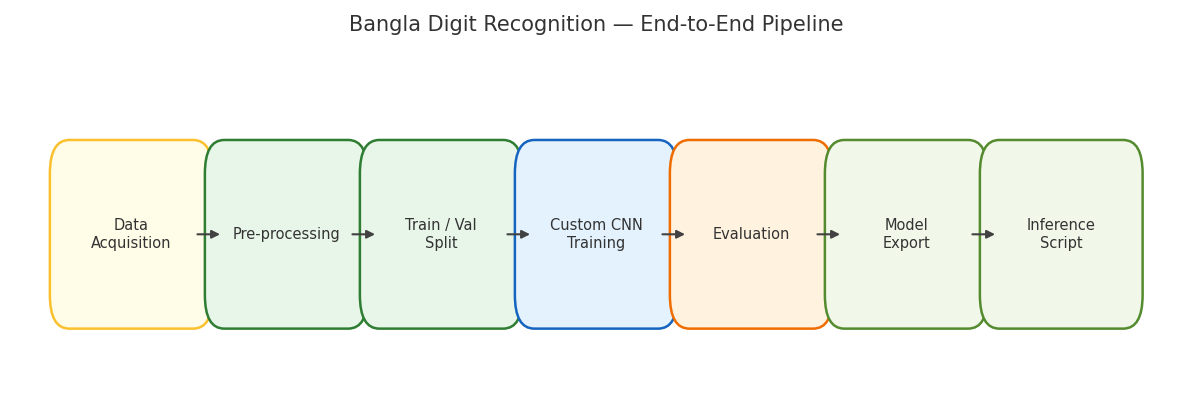
Introduction
Handwritten digit recognition is a fundamental challenge in computer vision that has applications ranging from digitizing historical documents to automating postal services. While Latin digit recognition has been thoroughly explored, Bangla (Bengali) digit recognition presents unique challenges due to the script’s distinctive features and the relative scarcity of large, standardized datasets.
In this blog post, we’ll explore a fascinating project that implements a Convolutional Neural Network (CNN) from scratch—without relying on deep learning frameworks—to recognize handwritten Bangla digits. We’ll delve into the neural network architecture, the mathematics behind it, the implementation details, and the results achieved.
Project Overview
The primary goal of this project is to build a convolutional neural network from the ground up that can accurately recognize handwritten Bangla digits. What makes this project particularly interesting is that it doesn’t use standard deep learning libraries like TensorFlow or PyTorch for the core neural network implementation. Instead, it constructs the entire CNN architecture using only NumPy, providing valuable insights into the inner workings of neural networks.
The project achieves an impressive 95.87% accuracy on the test dataset, demonstrating the effectiveness of the custom implementation.
Understanding the Dataset
The project uses the NumtaDB dataset, which contains handwritten Bangla digit images. You can find more information about this dataset at NumtaDB GitHub Repository.
The dataset is organized into multiple partitions:
- training-a
- training-b
- training-c
- training-d
- training-e
These partitions are combined and split into training and validation sets during the development process, with training-d often reserved for testing.
Each image in the dataset is a grayscale representation of a handwritten Bangla digit, and the corresponding labels are stored in CSV files that match the image filenames with their digit values (0-9).
Unique Characteristics of Bangla Digits
Bangla digits have distinct visual properties compared to Latin digits:
- More complex curved shapes and loops
- Higher variation in writing styles across the population
- Certain digits (like ১ and ৭) that can be easily confused
- More intricate details that require careful feature extraction
These characteristics make Bangla digit recognition a more challenging task that benefits from robust preprocessing and well-designed neural network architectures.
Image Preprocessing
Before feeding images into the neural network, several preprocessing steps are applied to enhance the model’s performance:
# Convert to grayscale
img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# Convert the image to binary using Otsu's thresholding
img = cv2.threshold(img, 0, 255, cv2.THRESH_BINARY + cv2.THRESH_OTSU)[1]
# Check if the background is black or white
# If the background is white, then invert the image
if np.mean(img) > 128:
img = 255 - img
# Dilate and erode to remove noise
kernel = np.ones((2, 2), np.uint8)
img = cv2.dilate(img, kernel, iterations=1)
img = cv2.erode(img, kernel, iterations=1)
These operations ensure that:
- All images are in grayscale format
- Thresholding converts grayscale images to binary (black and white)
- All images have a consistent background (black) and foreground (white) format
- Noise is reduced through morphological operations (dilation and erosion)
Additionally, the code removes empty rows and columns around the digit (where pixel intensity is near zero) and then resizes the image back to 28×28 pixels:
# Drop rows and columns with very low pixel values
row_drop = []
for i in range(img.shape[0]):
if 0 <= np.mean(img[i, :]) <= 5:
row_drop.append(i)
col_drop = []
for i in range(img.shape[1]):
if 0 <= np.mean(img[:, i]) <= 5:
col_drop.append(i)
# Drop the rows and columns
img = np.delete(img, row_drop, axis=0)
img = np.delete(img, col_drop, axis=1)
# Resize the image back to 28x28
img = cv2.resize(img, (28, 28), interpolation=cv2.INTER_AREA)
This centering process helps the model focus on the actual digit and ignore irrelevant empty space. For a deeper understanding of these image preprocessing techniques, you can visit OpenCV’s documentation on image processing.
Why These Preprocessing Steps Matter for Bangla Digits
The preprocessing pipeline is particularly effective for Bangla digits because:
-
Binarization with Otsu’s thresholding automatically determines the optimal threshold value, which is crucial for handling the varying stroke widths common in Bangla handwriting.
-
Background normalization ensures all digits have a consistent representation (white digits on black background), addressing the common inconsistency in how people write Bangla digits.
-
Morphological operations (dilation followed by erosion) help close small gaps in strokes that might otherwise break the connectivity of Bangla digits, which often contain delicate curves and connections.
-
Empty space removal centers the digit and maximizes its size within the frame, enhancing the model’s ability to detect the distinctive features of each Bangla numeral.
-
Final resizing to 28×28 standardizes all inputs while preserving the aspect ratio of the digit, which is critical for maintaining the proportional relationships in Bangla numerals.
CNN Architecture Details
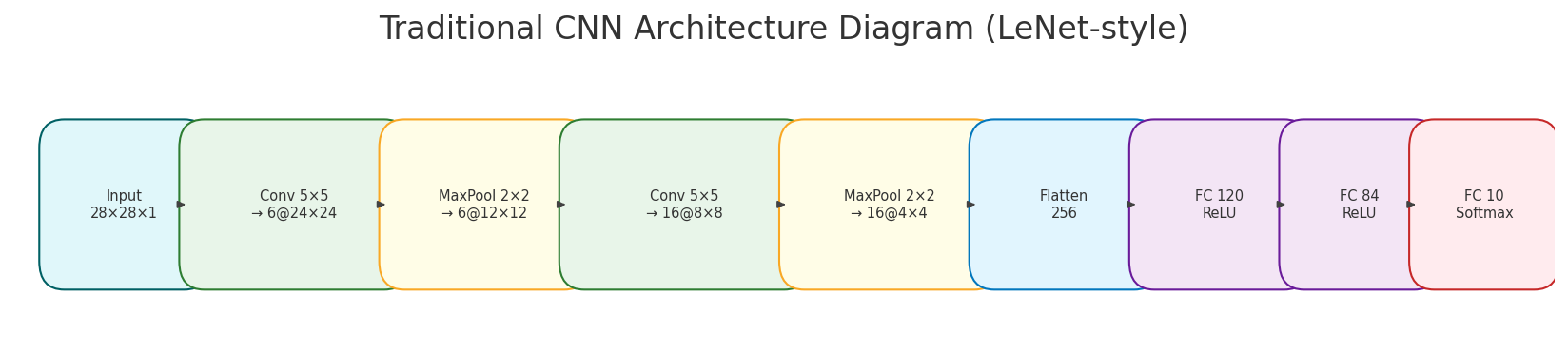
The project implements two different CNN architectures:
Architecture 1
- Input: 28×28×1 (grayscale images)
- Convolutional layer with 8 filters, followed by ReLU activation
- Max pooling layer
- Convolutional layer with 16 filters, followed by ReLU activation
- Max pooling layer
- Convolutional layer with 32 filters, followed by ReLU activation
- Max pooling layer
- Flatten layer
- Fully connected layer with 64 neurons and ReLU activation
- Output layer with 10 neurons and Softmax activation
Architecture 2 (LeNet-inspired)
- Input: 28×28×1 (grayscale images)
- Convolutional layer with 6 filters (5×5), followed by ReLU activation
- Max pooling layer (2×2, stride 2)
- Convolutional layer with 16 filters (5×5), followed by ReLU activation
- Max pooling layer (2×2, stride 2)
- Flatten layer
- Fully connected layer with 120 neurons and ReLU activation
- Fully connected layer with 84 neurons and ReLU activation
- Output layer with 10 neurons and Softmax activation
The second architecture, which appears to be inspired by the classic LeNet-5 architecture, is the one used in the final implementation shown in the training code. You can learn more about the original LeNet architecture at Yann LeCun’s website.
Why This Architecture Works Well for Bangla Digits
The LeNet-inspired architecture is particularly suitable for Bangla digit recognition for several reasons:
-
Hierarchical Feature Extraction: The gradual increase in filter numbers (6 → 16) allows the network to capture increasingly complex patterns, which is essential for Bangla digits that contain intricate shapes and curves.
-
Appropriate Field of View: The 5×5 convolution kernels provide a sufficient receptive field to capture the distinctive strokes and curves of Bangla digits without missing important details or including too much irrelevant information.
-
Dimensionality Reduction: The max pooling layers progressively reduce the spatial dimensions while preserving the most important features, making the model more computationally efficient and helping it focus on the most discriminative aspects of each digit.
-
Multi-stage Fully Connected Layers: The sequence of fully connected layers (120 → 84 → 10) provides sufficient complexity to learn the mapping from abstract features to specific digit classes, handling the subtleties that distinguish similar-looking Bangla digits.
-
Balanced Capacity: With approximately 61,706 trainable parameters (much smaller than modern deep networks), this architecture strikes a good balance between having enough capacity to learn complex patterns and avoiding overfitting on the limited dataset size.
Implementation from Scratch
The heart of this project is the implementation of the CNN from scratch using only NumPy. Let’s explore the key components:
Activation Functions
The project implements two activation functions:
ReLU (Rectified Linear Unit):
class ReLU():
def f(self, x):
return np.maximum(0, x)
def df(self, x, cached_y=None):
return np.where(x <= 0, 0, 1)
ReLU passes positive values unchanged and sets negative values to zero, allowing for efficient training of deep networks while mitigating the vanishing gradient problem. For a deeper mathematical understanding of activation functions, check out CS231n’s notes on activation functions.
Softmax:
class SoftMax():
def f(self, x):
y = np.exp(x - np.max(x, axis=1, keepdims=True))
return y / np.sum(y, axis=1, keepdims=True)
def df(self, x, cached_y=None):
return np.where(x <= 0, 0, 1)
The Softmax function converts a vector of real numbers into a probability distribution, making it ideal for the output layer in classification tasks. Note that subtracting the maximum value before taking the exponential is a numerical stability trick to prevent overflow.
Cost Function
The project uses the Softmax Cross-Entropy cost function:
class SoftmaxCrossEntropy():
def f(self, a_last, y):
batch_size = y.shape[0]
cost = -1 / batch_size * (y * np.log(np.clip(a_last, epsilon, 1.0))).sum()
return cost
def grad(self, a_last, y):
return - np.divide(y, np.clip(a_last, epsilon, 1.0))
This function computes the cross-entropy loss between the predicted probabilities and the true labels. The np.clip function prevents numerical instability by avoiding taking the logarithm of very small numbers. For more on cross-entropy loss, see Understanding Categorical Cross-Entropy Loss.
Optimization Algorithms
Two optimization algorithms are implemented:
Gradient Descent:
class GradientDescent():
def __init__(self, trainable_layers):
self.trainable_layers = trainable_layers
def initialize(self):
pass
def update(self, learning_rate, w_grads, b_grads, step):
for layer in self.trainable_layers:
layer.update_params(dw=learning_rate * w_grads[layer],
db=learning_rate * b_grads[layer])
This is the simplest optimization algorithm that updates weights by moving in the direction of the negative gradient scaled by the learning rate. Learn more about gradient descent at Sebastian Ruder’s optimization overview.
Adam (Adaptive Moment Estimation):
class Adam():
def __init__(self, trainable_layers, beta1=0.9, beta2=0.999, epsilon=1e-8):
self.trainable_layers = trainable_layers
self.v = {}
self.s = {}
self.beta1 = beta1
self.beta2 = beta2
self.epsilon = epsilon
# ... (initialization and update methods)
Adam is a more sophisticated algorithm that adapts the learning rate for each parameter based on estimates of first and second moments of the gradients. It’s generally more efficient than standard gradient descent. For an in-depth explanation of the Adam optimizer, check out the original paper by Kingma and Ba.
The Convolutional Layer Implementation
The most complex part of this project is the custom implementation of the convolutional layer:
class Conv():
def __init__(self, kernel_size, stride, n_c, padding='valid', activation=relu):
# ... initialization code ...
def forward(self, a_prev, training):
batch_size = a_prev.shape[0]
a_prev_padded = Conv.zero_pad(a_prev, self.pad)
out = np.zeros((batch_size, self.n_h, self.n_w, self.n_c))
# Convolve
for i in range(self.n_h):
v_start = i * self.stride
v_end = v_start + self.kernel_size
for j in range(self.n_w):
h_start = j * self.stride
h_end = h_start + self.kernel_size
out[:, i, j, :] = np.sum(a_prev_padded[:, v_start:v_end, h_start:h_end, :, np.newaxis] *
self.w[np.newaxis, :, :, :], axis=(1, 2, 3))
z = out + self.b
a = self.activation.f(z)
# ... caching for backward pass ...
return a
This implementation:
- Pads the input based on the padding strategy (‘valid’ or ‘same’)
- Initializes an output volume of appropriate dimensions
- Uses nested loops to slide the kernel across the input volume
- Computes the dot product between the kernel and each patch of the input
- Adds the bias term and applies the activation function
Why this custom implementation is particularly effective:
-
Direct Control: By implementing the convolution operation directly, the code has complete control over how features are extracted, which allows for custom optimizations specific to Bangla digits.
-
Transparency: The explicit loop-based implementation makes it clear exactly how the convolution operates, without any “magic” happening inside library functions.
-
Educational Value: This approach forces a deep understanding of how CNNs work, which can lead to more thoughtful architecture design.
-
Flexibility: The implementation can be easily modified to handle specific challenges of Bangla digit recognition if needed.
Backpropagation Through the Convolutional Layer
The backward pass through the convolutional layer is equally important:
def backward(self, da):
batch_size = da.shape[0]
a_prev, z, a = (self.cache[key] for key in ('a_prev', 'z', 'a'))
a_prev_pad = Conv.zero_pad(a_prev, self.pad) if self.pad != 0 else a_prev
da_prev = np.zeros((batch_size, self.n_h_prev, self.n_w_prev, self.n_c_prev))
da_prev_pad = Conv.zero_pad(da_prev, self.pad) if self.pad != 0 else da_prev
dz = da * self.activation.df(z, cached_y=a)
db = 1 / batch_size * dz.sum(axis=(0, 1, 2))
dw = np.zeros((self.kernel_size, self.kernel_size, self.n_c_prev, self.n_c))
# 'Convolve' back
for i in range(self.n_h):
v_start = self.stride * i
v_end = v_start + self.kernel_size
for j in range(self.n_w):
h_start = self.stride * j
h_end = h_start + self.kernel_size
da_prev_pad[:, v_start:v_end, h_start:h_end, :] += \
np.sum(self.w[np.newaxis, :, :, :, :] *
dz[:, i:i+1, j:j+1, np.newaxis, :], axis=4)
dw += np.sum(a_prev_pad[:, v_start:v_end, h_start:h_end, :, np.newaxis] *
dz[:, i:i+1, j:j+1, np.newaxis, :], axis=0)
dw /= batch_size
# ... handle padding for da_prev ...
return da_prev, dw, db
This implementation:
- Computes the gradient of the loss with respect to the pre-activation (
dz) - Calculates the gradient with respect to the weights (
dw) and biases (db) - Computes the gradient flowing back to the previous layer (
da_prev) - Handles padding appropriately to ensure dimensions match
For a more detailed explanation of backpropagation in CNNs, see CS231n’s notes on backpropagation.
Why This Implementation Works So Well
The custom CNN implementation achieves an impressive 95.87% accuracy on Bangla digit recognition for several key reasons:
1. Appropriate Architecture Design
The LeNet-inspired architecture used in this project is particularly well-suited for digit recognition tasks. Originally designed for handwritten digit recognition (albeit for Latin digits), LeNet’s structure provides an excellent starting point for Bangla digits as well. The sequence of convolutional layers, pooling layers, and fully connected layers creates a hierarchical feature extraction process that can identify the distinctive patterns in Bangla numerals.
2. Effective Preprocessing Pipeline
The preprocessing steps are carefully designed to enhance the quality of the input images:
- Binarization: Converting the images to binary format reduces noise and focuses on the essential structure of the digits.
- Standardization: Ensuring all digits have consistent foreground/background representation eliminates one source of variation that the model doesn’t need to learn.
- Morphological operations: Dilation and erosion help repair broken strokes and remove small noise artifacts, which is particularly important for Bangla digits with their complex structures.
- Empty space removal and centering: This helps the network focus on the actual digit content rather than wasting capacity learning to ignore empty regions.
3. Numerical Stability Techniques
The implementation incorporates several techniques to ensure numerical stability:
- Subtracting the maximum value in Softmax: This prevents overflow when computing exponentials.
- Clipping small values in the cross-entropy calculation: This avoids taking logarithms of values very close to zero.
- Proper weight initialization: Using the He initialization method (scaled by sqrt(2/n)) helps ensure proper gradient flow during the initial phases of training.
4. Batch Normalization Through Mini-Batches
The use of mini-batch training (with a batch size of 200) provides a form of regularization and helps the model generalize better. It also allows for more frequent weight updates, which can lead to faster convergence.
5. Careful Hyperparameter Selection
The learning rate (0.005) and number of epochs (30) have been carefully chosen to balance training speed with accuracy. The relatively small learning rate ensures stable training, while the number of epochs provides sufficient time for the model to converge without overfitting.
6. Robust Evaluation Metrics
Using multiple evaluation metrics (accuracy, F1 score, and confusion matrix) provides a comprehensive view of the model’s performance, helping to identify and address potential issues with specific digits.
Performance Optimization Techniques
The implementation employs several techniques to optimize performance:
1. Weight Initialization
The weights are initialized using the He initialization method, which is particularly well-suited for ReLU activations:
self.w = np.random.randn(self.kernel_size, self.kernel_size, self.n_c_prev, self.n_c) * \
np.sqrt(2 / (self.kernel_size * self.kernel_size * self.n_c_prev))
This initialization strategy helps ensure that activations neither vanish nor explode at the beginning of training, allowing for faster convergence. For more on weight initialization strategies, see Understanding Xavier Initialization in Deep Neural Networks.
2. Mini-Batch Training
The model is trained using mini-batches rather than full-batch or stochastic gradient descent:
cnn.train(x_train, y_train,
mini_batch_size=200,
learning_rate=0.005,
num_epochs=30,
validation_data=(x_test, y_test))
Mini-batch training strikes a balance between computational efficiency and update stability. It also introduces a form of regularization that can help the model generalize better.
3. Learning Rate Selection
The learning rate (0.005) has been carefully chosen to be:
- Small enough to ensure stable convergence without overshooting minima
- Large enough to allow the model to make meaningful progress in a reasonable number of epochs
4. Caching During Forward Pass
To improve the efficiency of backpropagation, the implementation caches activations and intermediate values during the forward pass:
if training:
# Cache for backward pass
self.cache.update({'a_prev': a_prev, 'z': z, 'a': a})
This eliminates the need to recompute these values during the backward pass, significantly improving computational efficiency.
Applications and Future Directions
This Bangla handwritten digit recognition system has numerous practical applications:
Immediate Applications
-
Document Digitization: Converting handwritten Bangla documents into digital text, preserving cultural and historical materials.
-
Postal Automation: Automating the sorting and routing of mail based on handwritten Bangla postal codes and addresses.
-
Educational Tools: Creating interactive learning systems to help students practice writing Bangla numerals with real-time feedback.
-
Banking Systems: Processing handwritten Bangla digits on checks, forms, and other financial documents.
-
Form Processing: Automating the entry of handwritten numerical data from forms in government offices, healthcare facilities, and businesses.
Future Directions
-
Extending to Bangla Characters: The system could be extended to recognize full Bangla script, not just digits.
-
Real-time Recognition: Optimizing the implementation for real-time recognition on mobile devices or embedded systems.
-
Multi-script Recognition: Developing a system that can handle multiple scripts (Bangla, Latin, Devanagari, etc.) simultaneously.
-
Integration with OCR Systems: Incorporating this digit recognition system into a full Optical Character Recognition pipeline for Bangla documents.
-
Transfer Learning Approaches: Exploring how pre-trained models on Latin digits could be adapted for Bangla digits with minimal retraining.
Conclusion
This project demonstrates that it’s possible to build a highly effective neural network from scratch using only NumPy, without relying on deep learning frameworks. By achieving an accuracy of 95.87% on Bangla handwritten digit recognition, it shows that a well-designed architecture with appropriate preprocessing can perform exceptionally well even without the advanced optimizations provided by modern deep learning libraries.
The implementation provides valuable insights into the inner workings of convolutional neural networks, including forward and backward propagation, various layer types, and optimization algorithms. It serves as both a practical solution for Bangla digit recognition and an educational resource for those wanting to understand the fundamentals of neural networks.
As AI applications continue to expand globally, projects like this that focus on languages beyond English make technology more inclusive and accessible to diverse populations. The techniques and insights from this project can inspire similar efforts for other scripts and languages, contributing to a more equitable technological landscape.